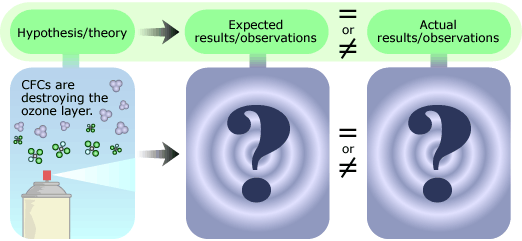
To overcome skepticism and convince other scientists and policymakers of the importance of the Molina-Rowland hypothesis, they needed to test their ideas with actual atmospheric evidence. However, figuring out just what evidence to look for was tricky. Sometimes the expectations generated by a particular hypothesis are obvious (e.g., if you hypothesize that smoking causes lung cancer, you’d expect smokers to have higher rates of lung cancer than non-smokers) — but in this case, it was much more complicated. In fact, atmospheric interactions are so complex that the full implications of the hypothesis couldn’t be worked out by hand. Instead, scientists relied on mathematical models of the atmosphere which could be studied using computers.
WHAT’S A MATHEMATICAL MODEL?
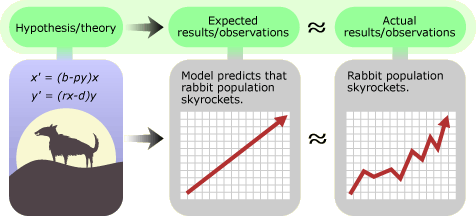
“Model” can mean several different things in science, but as a research method, modeling often means creating a mathematical model — a set of equations that represents a real system. That system could be any aspect of the natural world — from the movement of molecules in a balloon, to the connections among neurons in your brain, to the interactions among species in an ecosystem. For example, a simple mathematical model of a species interaction might describe how the number of rabbits is related to the birth rate of the rabbits and the number of wolves present. A more complex model of the same system could include more information, such as the effects of hunting, how the number of rabbits affects the wolves’ birthrate, and how rabbit grazing affects their food supply. Though scientists try to limit the factors represented in models to the ones essential for their purposes, these sets of equations are often so complex that they require a computer to solve.

To create a mathematical model, scientists must first gather all the relevant information on the system. In the case of the ecosystem model, this might mean knowledge of how rabbits and wolves interact. Atmospheric models relating to CFCs, on the other hand, were based on information about how molecules move through the atmosphere, what chemical reactions occur there, the concentrations of the atmosphere’s chemical constituents, etc. This information was combined with basic principles, like conservation of energy, to create a set of equations that represents the behavior of the real-world system — the atmosphere.
Models are based on sets of hypotheses about how a system works. The wolf-rabbit model is essentially a hypothesis about how the two species interact and how these interactions affect their numbers. The CFC-atmosphere models represent a set of hypotheses about how molecules interact with one another as they move through the atmosphere. Models, and the hypotheses within them, are supported when the model generates expectations that match the behavior of its real-world counterpart — e.g., if removing hunting from the model has a similar effect to that observed in the real world when wolves are protected from hunting. If a model is supported and seems to be a good representation of the real world, we can use it to answer “what if” questions: What would happen to rabbit populations if we allowed wolf hunting in particular areas — or more pertinently for Molina and Rowland, what would happen in 50 years if we continued CFC production at 1974 rates?
Several groups of scientists added Molina and Rowland’s proposed set of reactions to their models of the atmosphere, and used the models to generate expectations about what should be going on in the atmosphere if the model and reactions were correct. Now, they just needed to find out if observations matched the models’ predictions …
Scientists studied Rowland and Molina’s hypothesis using mathematical models. For more information on how scientists create and use models, visit Visionlearning’s module on Modeling as a research method.